[Tensorflow] 5. Logistic Regression
Logistion Regression
1. Classification
일상생활에서는 case가 분류되는 경우가 많다. 예를들면,시험 : 합격 / 탈락
메일분류 : 스팸메일 / 일반 메일
이렇게 두가지 케이스로 분류 되는 경우를 Binary Classification 이라고 한다. 이후 Multi-class 또한 다룰 것이다.
2. Logistic Regression
앞서 배운 Linear Regression과의 차이점은 아래의 그래프를 보면 명확하게 보인다. Logistic에 사용되는 데이터를 보면 값들이 불연속적이고 데이터의 구분이 명확하다. 그에 반에 Linear 에 사용되는 데이터들은 시간, 신장 처럼 다양한 값들이 수치형으로 나타난다.따라서 Logistic Regression의 데이터들은 [0] 과 [1] 로 (아래 그래프를 예로 들면, 네모와 세모) 구분지을 수 있고 Linear Regression 은 실제 데이터 값들을 수치형으로 사용하게 된다.
구하는 data의 값을 hypothesis 함수에 넣으면 우리가 필요로 하지 않는 연속적인 수치화된 값이 얻어진다. 이를 우리가 원하는 방향으로 사용하기 위해서 새로운 함수가 필요한데 이것을 Regression Function이라고 하고 이 함수를 거치고 나면 0 또는 1 로 데이터가 분류 된다.
보통 Regression Function은 g(z)로 다음과 같이 정의된다.
함수를 보면 한쪽은 1에 다른 한 쪽은 0에 수렴하고 있음을 알 수 있다. 이 함수를 시그모이드 함수(sigmoid) 라고 부른다. 함수를 통해 계산되는 0과 1 사이의 값은 정의되는 Decision Boundary를 기준으로 바운더리 이상은 1, 이하는 0 과 같이 분류된다. decision boundary는 하나의 실수가 될 수도 있고, 하나의 수식이 될 수도 있다.
3. Cost Function
Logistic Regression을 구현하기위해서도 Cost를 최소화하는 함수가 필요하다. 먼저 주어진 데이터를 통해 모델을 학습시켜 최적의 모델을 찾는 과정은 Linear Regression에서 했던 것과 원리가 같다.
고등학생 때 배웠던 로그 함수를 기억해보자. 1을 기준으로 1보다 작은 경우 마이너스 무한대로 감소한다. 따라서 0과 1로 나눠지는 y 값에 대해서 log 함수를 취하면 위 그림과 같이 y가 1일때 1에 가까워 질수록 cost가 작아지고, y가 0일때 가설 값도 0에 가까워질때 cost가 작아지는 cost 함수가 만들어진 것을 알 수 있다. 두가지를 합치면 convex 함수, 즉 가운데가 볼록한 하나의 최적화된 함수를 구할 수 있는 cost function이 나온다. 이 convex function의 gradient (경사값)을 구하는 과정을 반복하여 최소값이 나오는 최적의 모델을 구하는 것을 Optimization이라 부른다.
4. 예제 실습
텐서플로우로 Logistic Regression을 직접 구현해본다. 먼저 이번 예제 코드에서 사용되는 몇가지 개념들이 있는데 그것부터 짚고 넘어가겠다.
- epoch
한 번의 epoch 란 '인공 신경망에서 전체 데이터 셋에 대해 forward pass/backward pass 과정을 거친 것을 말한다. 즉, 전체 데이터 셋에 대해 한 번 학습을 완료한 상태'이다.
- batch size / iteration
한 번의 batch마다 주는 데이터 샘플의 size. 여기서 batch는 나눠진 데이터 셋을 뜻하며, iteration은 epoch를 나누어서 실행하는 횟수라고 생각하면 된다.
- Dataset
tf.data.Dataset으로 사용하며 텐서플로우 Estimator모델에서 사용되는 데이터 입력 파이프라인이다. 사용 예를 보면
x = np.random.sample((10, 2))
dataset = tf.data.Dataset.from_tensor_slices(x)
위와 같은 방식으로 Dataset을 생성할 수 있는데 tf.data.Dataset.from_tensor_slices() 함수는 Dataset을 생성하는 함수로, 입력된 텐서로부터 slices를 생성한다.
데이터를 입력하는 방법으로는 placeholder 데이터 구조에 feed 하는 방식도 많이 쓰인다. 하지만 텐서플로우 공식 홈페이지를 참고해보면 'Feeding'은 가장 비효율적인 데이터 입력 방식이라고 한다. 텐서플로우에서 사용을 권장하는 효율적인 모듈이 tf.data이다.
tf.data는 대규모 데이터 feeding용 모듈이다. 여러가지 방식으로 데이터를 불러 올 수 있지만 가장 기본적인 방법은 generator로 데이터를 불러오는 from_generator() 메서드를 이용하는 것이다. 모듈에서 batch size도 바로 지정할 수 있다. (하지만 이번 예제에서는 대규모 데이터가 아닌 아주 적은 데이터를 학습용으로 사용하기 때문에 slices를 이용해 dataset에 넣기만 한다.)
-- 소스 코드 --
1
2
3
4
5
6
7
8
|
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
import tensorflow as tf
tf.enable_eager_execution()
tf.set_random_seed(777)
print(tf.__version__)
| cs |
수강하고 있는 강의와 같은 환경에서 실습을 진행하기 위해 나는 tensorflow1.12.0을 사용한다. matplotlib.pyplot은 밑에서 그래프를 그리기 위해 import한 것이다.
Tensorflow Eager Execution은 텐서플로우를 대화형 명령 스타일로 프로그래밍 할 수 잇도록 해주는 것으로 텐서플로우를 보다 쉽게 시작할 수 있으며 개발을 더 직관적으로 할 수 있다. eager execution에서 텐서는 데이터를 직접 포인팅하기 때문에 tf.Session을 시작하지 않아도 직접 값을 얻을 수 있다. 다시말하면 eager execution은 기존의 그래프 방식에서 벗어나 그래프의 생성 없이 연산을 즉시 실행하는 명령형 프로그래밍 환경을 뜻한다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
|
##x_data는 2차원 배열 데이터, y_data는 0과 1로 구분된다
x_train= [[1., 2.],
[2., 3.],
[3., 1.],
[4., 3.],
[5., 3.],
[6., 2.]]
y_train = [[0.],
[0.],
[0.],
[1.],
[1.],
[1.]]
x_test=[[2.,2.]]
y_test=[[0.]]
x1 = [x[0] for x in x_train]
x2 = [x[1] for x in x_train]
| cs |
x_train은 학습 data로 주어질 (x1,x2) 데이터이고 y_train은 x_train들이 각각 0과 1로 분류 되는 것을 나타내는 data이다. test해 볼 데이터는 (2,2) 데이터가 '0' 으로 맞게 분류되는가 이다. 다음은 데이터들을 한 눈에 들어오게 가시화 하는 부분이다. 꼭 필요한 부분은 아니므로 생략해도 좋다.
1
2
3
4
5
6
7
|
colors = [int(y[0]%3) for y in y_train]
plt.scatter(x1,x2, c=colors, marker='^')
plt.scatter(x_test[0][0],x_test[0][1],c="red")
plt.xlabel("x1")
plt.ylabel("x2")
plt.show()
| cs |
검은 세모들이 0, 노란 세모들이 1 로 분류 된 것이다. 빨간 점이 우리가 테스트 하고자하는 데이터이므로 0으로 분류한 것이 옳다고 나와야 이 모델이 적합한 판단을 한다고 할 수 있을 것이다.
1
2
|
dataset = tf.data.Dataset.from_tensor_slices((x_train, y_train)).batch(len(x_train))
#batch size는 한 번에 학습시킬 size로 정한다
| cs |
위에서 설명했던 dataset을 정의하는 부분이다. x_train과 y_train을 dataset 모듈로 feed 해주고 batch size는 한 번에 학습시킬 size인 x_train의 길이로 지정해준다.
1
2
|
W = tf.Variable(tf.zeros([2,1]),name='weight')
b = tf.Variable(tf.zeros([1]),name='bias')
| cs |
Weight는 6x2 matrix인 x_train과 dot 연산을 해야 하기 때문에 2x1로 만들어준다.
1
2
3
|
def logistic_regression(features):
hypothesis = tf.div(1.,1.+tf.exp(tf.matmul(features,W) + b ))
return hypothesis
| cs |
sigmoid 함수를 수식으로 구현한 것이다. 간단하게 tf.sigmoid(tf.matmul(features,W)+b)
로도 구현 가능하다.
1
2
3
4
5
|
def loss_fn(hypothesis, features, labels):
cost = -tf.reduce_mean(labels*tf.log(hypothesis)+(1-labels)*tf.log(1-hypothesis))
return cost
optimizer = tf.train.GradientDescentOptimizer(learning_rate=0.01)
| cs |
𝑐𝑜𝑠𝑡(ℎ(𝑥),𝑦)=−𝑦𝑙𝑜𝑔(ℎ(𝑥))−(1−𝑦)𝑙𝑜𝑔(1−ℎ(𝑥))
cost 수식을 텐서플로우로 구현한 부분이다. 아래는 cost를 최소화하는 optimizer로 앞서 배운 GradientDescent를 사용하는 부분이다.
1
2
3
4
5
|
# sigmoid 함수값이 0.5 이상이 나오면 1, 그 이하는 0이 나오도록 지정
def accuracy_fn(hypothesis,labels):
predicted = tf.cast(hypothesis > 0.5,dtype=tf.float32)
accuracy = tf.reduce_mean(tf.cast(tf.equal(predicted,labels),dtype=tf.int32))
return accuracy
| cs |
sigmoid 함수를 통해 나온 값으로 0 / 1 로 구분하는 부분이다. 그리고 참 값(labels=y_train)과 비교하여 평균을 잡아 그것을 accuracy로 보는 것이다.
1
2
3
4
|
def grad(hypothesis,features,labels):
with tf.GradientTape() as tape:
loss_value = loss_fn(logistic_regression(features),features,labels)
return tape.gradient(loss_value, [W,b])
| cs |
GradientTape 모듈을 이용하여 경사하강법을 적용하여 최적의 모델을 찾는다.
1
2
3
4
5
6
7
8
9
10
|
EPOCHS = 1001
for step in range(EPOCHS):
for features, labels in iter(dataset):
grads = grad(logistic_regression(features),features,labels)
optimizer.apply_gradients(grads_and_vars=zip(grads,[W,b]))
if step % 100 ==0:
print("Iter: {}, Loss: {:.4f}".format(step,loss_fn(logistic_regression(features),features,labels)))
test_acc = accuracy_fn(logistic_regression(x_test),y_test)
print("Testset Accuracy: {:.4f}".format(test_acc))
| cs |
1000번 반복하면서 위에서 정의한 메소드들을 이용해 최적의 모델을 찾는과정이다. 출력은 100번째 마다 cost를 출력하도록 하였다. 1000번의 최적화가 끝난 모델로 test 할 data들을 입력한다.
'0' 일 것이라고 예상한 결과와 Accuracy가 일치함을 볼 수 있다.



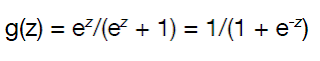




![[Tensorflow] 5. Logistic Regression](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEj41-lm90ZhMqWNcefdc0r0JVA82joe_818Jej1aZU5hxF9WUWu7sf69zVrDZzykD_w88kaIXGPxy5VJaqDmiLqvD96YWHF4FnpS4nmj9q7uO75NZ-L2BNpvebEuG4f9D5LC94irIqTUD0/s72-c/9.PNG)

No comments: